CHƯƠNG I. PHÉP DỜI HÌNH VÀ PHÉP ĐỒNG DẠNG TRONG MẶT PHẲNG

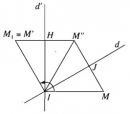
Bài 1.21 trang 30 Sách bài tập (SBT) Hình học 11

Chứng minh rằng mỗi phép quay đều có thể xem là kết quả của việc thực hiện liên tiếp hai phép đối xứng trục.

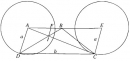
Bài 1.22 trang 30 Sách bài tập (SBT) Hình học 11

Cho hình vuông ABCD có tâm I. Trên tia BC lấy điểm E sao cho BE = AI.

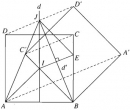
Bài 1.30 trang 39 Sách bài tập (SBT) Hình học 11

Cho hình thang ABCD có AB song song với CD, AD = a, DC = b còn hai đỉnh A, B cố định. Gọi I là giao điểm của hai đường chéo.

Bài 1.23 trang 35 Sách bài tập (SBT) Hình học 11

Hãy viết phương trình của đường thẳng d1 là ảnh của d qua phép vị tự tâm O tỉ số k = 3

Bài 1.24 trang 35 Sách bài tập (SBT) Hình học 11

Trong mặt phẳng tọa độ Oxy cho đường tròn (C) có phương trình

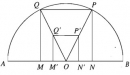
Bài 1.25 trang 35 Sách bài tập (SBT) Hình học 11

Cho nửa đường tròn đường kính AB. Hãy dựng hình vuông có hai đỉnh nằm trên nửa đường tròn, hai đỉnh còn lại nằm trên đường kính AB của nửa đường tròn đó.

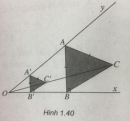
Bài 1.26 trang 35 Sách bài tập (SBT) Hình học 11

Cho góc nhọn xOy và điểm C nằm trong góc đó. Tìm trên Oy điểm A sao cho khoảng cách từ A đến Ox bằng AC.

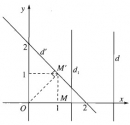
Bài 1.27 trang 38 Sách bài tập (SBT) Hình học 11

Hãy viết phương trình đường thẳng d’ là ảnh của d qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O

Bài 1.28 trang 38 Sách bài tập (SBT) Hình học 11

Hãy viết phương trình đường tròn (C’) là ảnh của (C) qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k = -2 và phép đối xứng qua trục Ox

Bài 1.29 trang 38 Sách bài tập (SBT) Hình học 11

Chứng minh rằng hai đa giác đều có cùng số cạnh luôn đồng dạng với nhau

Bài 1.31 trang 39 Sách bài tập (SBT) Hình học 11

Hãy viết phương trình đường thẳng d’ là ảnh của d qua phép tịnh tiến theo vectơ

Bài 1.32 trang 39 Sách bài tập (SBT) Hình học 11

Cho hình bình hành ABCD có AB cố định, đường chéo AC có độ dài bằng m không đổi. Chứng minh rằng khi C thay đổi, tập hợp các điểm D thuộc một đường tròn cố định.

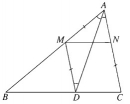
Bài 1.33 trang 39 Sách bài tập (SBT) Hình học 11

Cho tam giác ABC. Tìm một điểm M trên cạnh AB và một điểm N trên cạnh AC sao cho MN song song với BC và AM = CN.

Bài 1.34 trang 39 Sách bài tập (SBT) Hình học 11

a) Viết phương trình của đường thẳng d1 là ảnh của d qua phép đối xứng qua trục Oy

Bài 1.35 trang 39 Sách bài tập (SBT) Hình học 11

Cho đường tròn (C) và hai điểm cố định phân biệt A, B thuộc (C).

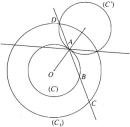
Bài 1.36 trang 39 Sách bài tập (SBT) Hình học 11

Hãy dựng đường thẳng qua A cắt đường tròn bán kính r tại B, cắt đường tròn bán kính R tại C, D

Bài 1.37 trang 39 Sách bài tập (SBT) Hình học 11

Hãy viết phương trình của đường thẳng d’ là ảnh của d qua phép quay tâm O góc 45°.

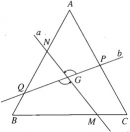
Bài 1.38 trang 40 Sách bài tập (SBT) Hình học 11

Chứng minh rằng tứ giác MNPQ là một hình thang cân.

Bài 1.39 trang 40 Sách bài tập (SBT) Hình học 11

Gọi A', B', C' tương ứng là ảnh của ba điểm A, B, C qua phép đồng dạng tỉ số k. Chứng minh rằng:

Bài 1.40 trang 40 Sách bài tập (SBT) Hình học 11

Gọi A’, B’ và C’ tương ứng là ảnh của ba điểm A, B và C qua phép đồng dạng.

Các mục con